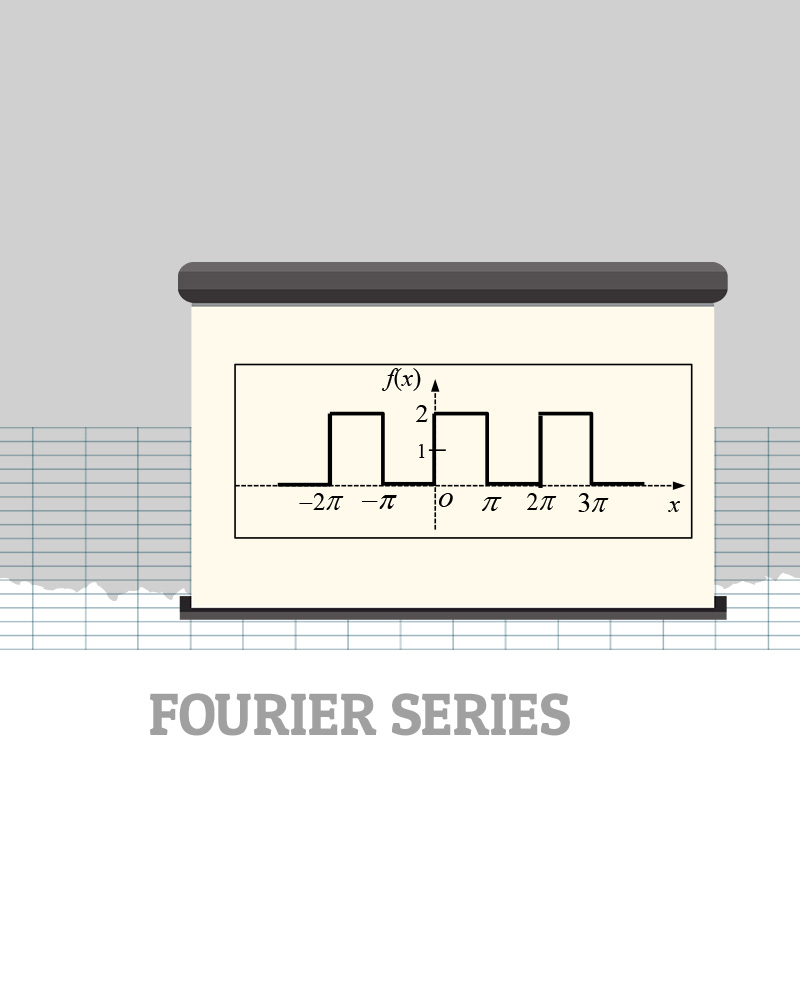
Before looking at the example, you need to know the formula of Fourier Series as shown.
If you know the additional information shown, you could reduce your work. (1) Odd functions have Fourier Series with only sine terms, which means you only find the coefficients, b’s in the formula. (2) Even functions have Fourier Series with cosine and possible constant terms., which means you only find the coefficients, a’s in the formula.